C’est quoi le problème ?
On désigne par tableau de contingence un tableau de dénombrement où une population est répartie suivant deux critères qualitatifs.
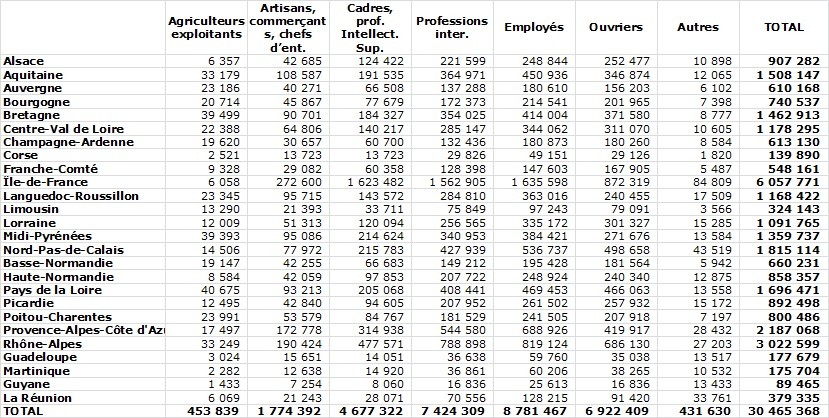
Dans le tableau ci-dessous, par exemple, la population active est répartie par région et catégorie professionnelle (tableau INSEE 2012).
Face à un tableau comme celui-ci, la question est de savoir comment mettre en évidence rapidement les chiffres importants ? Le plus souvent, l’analyse consiste à ramener ce type tableau à des pourcentages par exemple, on calculera le pourcentage que représente chaque catégorie dans le total régional. Ce type de transformation fait ressortir certains chiffres : importance des cadres et professions intellectuelles en Ile de France et faiblesse de cette même catégorie dans les DOM, …
Dans le tableau ci-dessus on a appliqué à chaque colonne deux formats conditionnels : mise en couleur des 3 plus grandes valeurs en rouge et des 3 plus petites en vert (Onglet Accueil, bouton Mise en forme conditionnelle, Règle des valeurs plus/moins élevées, x valeurs les plus (resp. moins) élevées …). L’application de formats conditionnels améliore notablement la lisibilité des tableaux.
C’est déjà un résultat, mais on peut être plus exigent en demandant quelles sont les cellules du tableau qui contiennent le plus d’information.
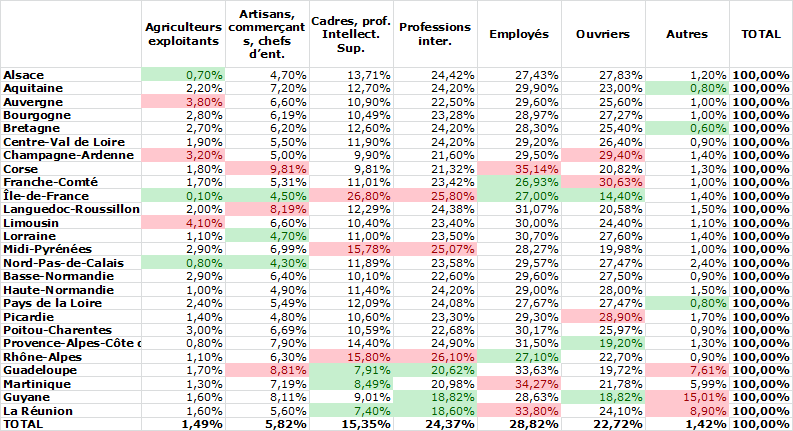
Avant de répondre à cette question, transformons notre tableau initial en le ramenant à des pourcentages. Chaque cellule du nouveau tableau est obtenue en divisant l’effectif du tableau initial par l’effectif total. Ce calcul est valide autant pour les cellules internes du tableau que pour les totaux de lignes ou de colonnes. Ainsi, la population active d’Ile de France (6 057 771 personnes) représente 19,88 % du total : 6 057 771 / 30 465 368.
Information ? Kesako ?
Il existe de multiples définitions du mot information. Dans le cas qui nous occupe, je donnerai la suivante : l’information est la différence entre ce qui est attendu et ce qui est.
Intéressons-nous à ce qui est attendu.
Supposons que la région et la répartition sur différentes catégories professionnelles soient indépendantes l’une de l’autre. On s’attendrait alors à ce que la répartition en catégories professionnelles soit à peu près la même dans chaque région, le nombre d’actifs dans chaque catégorie étant proportionnel lui-même à la part de la région dans le total national.
Cette hypothèse d’indépendance est bien évidemment démentie par la réalité. On imagine facilement que la proportion d’agriculteurs dans la population active est plus faible en Ile de France que dans le Limousin. Mais elle va nous permettre d’établir un tableau auquel comparer notre réalité.
Nous avons construit le tableau ci-dessous en appliquant l’hypothèse d’indépendance (Pour plus de visibilité on n’en présente qu’un extrait).
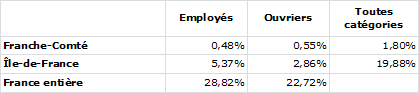
Dans ce nouveau tableau, on a conservé les pourcentages que représentent chaque ligne et chaque colonne dans la réalité. On a calculé ensuite pour chaque case (en italique) le produit du « total » de la ligne et du « total » de la colonne auxquelles cette case appartient. En effet, nous l’avons dit plus haut, si région et catégorie professionnelle sont indépendantes l’une de l’autre, le pourcentage que représente chaque case par rapport au total général est proportionnel au pourcentage que représente la catégorie et au pourcentage que représente la région, soit le produit de l’un par l’autre. Ainsi la proportion d’employés dans la population active étant de 28,82 % et l’Ile de France représentant 19,88 % de la population active totale, on s’attend à ce que les employés d’Ile de France représentent 5,73 % de la population active française.
Voici donc pour ce qui est attendu. Comparons à présent ce tableau la réalité (Tableau 1).
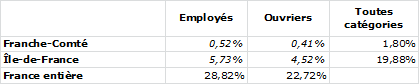
Certaines cases (Employés de Franche-Comté 0,52 % attendus contre 0,48 % en réalité) ont des valeurs assez proches dans les deux tableaux. La proportionnalité semble s’appliquer comme si catégories et régions étaient indépendantes. La valeur de la case s’obtenant par simple multiplication elle ne recèle pas d’information propre.
D’autres cases, en revanche, présentent des différences importantes (Ouvriers d’Île-de-France 4,52 % attendus contre 2,86 % en réalité). Cette différence est l’indice de phénomènes qui ont créés cette distorsion entre attente et réalité. Cet indice, c’est l’information que nous donne cette case. C’est au spécialiste de déterminer quels sont les phénomènes agissant.
Il est toujours possible, évidemment, que pour une case, deux phénomènes agissant de manière opposée aboutissent à une réalité proche de ce qui est attendu. La statistique ne peut rien dans ce cas.
Le jeu des différences
Bien qu’il existe une démonstration rigoureuse et cohérente avec la théorie de l’information, on s’en tiendra à la constatation intuitive : différence = information. Plus la répartition réelle présente de différence avec la répartition attendue plus le tableau recèle d’information. Nous verrons dans un prochain article qu’il est possible de quantifier les différences et d’ordonner ainsi rigoureusement les cases de notre tableau par apport d’information décroissant. Quelle perspective exaltante, n’est-ce pas ?
D’ici là, peut-être avez-vous des tableaux de contingence qui trainent dans classeurs ? Il est temps de porter sur eux un regard nouveau.

Bonjour Frédérique,
Il n’y pas de fonction qui donne immédiatement ce résultat. Il y a plusieurs formules qui le donnent en voici 2 mais elles sont un peu tarabiscotées.
On supposera que la colonne A contient les valeurs à compter (s’il y a un en-tête, soustraire 1 au résultat)
1ère : =SOMME((FREQUENCE(A:A;A:A)>0)*1)
La fonction fréquence compte les valeurs compte les valeurs (dans la plage passée en paramètre 1) contenues dans les intervalles définis par le paramètre 2. Si une valeur se répète, la fonction n’en retient qu’une fois le compte (on a 0 ensuite). Dans votre exemple la fonction renverra 2 pour le premier 10 et 0 pour le second. La comparaison >0 permet de renvoyer vrai ou faux. La multiplication par 1 permet de transformer VRAI en 1 et Faux en 0. Il suffit alors de totaliser.
2ème : moins élégante et moins rapide mais plus compréhensible {=SOMME(si(A:A<> » »;1/NB.SI(A:A;A:A);0))}
Les accolades ne se saisissent pas. On les obtient en validant la formule avec la combinaison de touche Ctrl + Maj + Entrée au lieu d’Entrée. La formule obtenue est matricielle, c’est à dire qu’elle exécute les actions sur toute une plage.
NB/SI() compte le nombre de fois que chaque valeur intervient dans la plage. 10 intervient 2 fois, 1/NB.SI() vaut 1/2. Comme on additionne toutes les valeurs obtenues, pour chaque valeur distincte on additionne n fois la valeur 1/n. Le test SI évite juste de prendre en compte les cellules vides qui mettent la formule en erreur.
N.B. FREQUENCE a elle-même un comportement matriciel.
J’ai essayé d’être clair mais même si certains aspects restent nébuleux, l’écriture exacte des formules vous donnera votre résultat.