Analyse des tableaux de contingence (suite et fin)

Mesurer l’écart entre l’attendu et le réel

Dans l’article précédent nous avons vu que nous pouvions à partir d’un tableau de contingence, avec les sommes des colonnes et des sommes des lignes de ce tableau, établir un autre tableau donnant la distribution attendue dans le cas où les deux critères d’analyses sont indépendants. Bien que cette hypothèse d’indépendance soit fausse dans le cas étudié, elle nous a permis d’établir un tableau auquel comparer notre réalité. Nous avons conclus que les différences entre le réel et l’attendu sont l’expression de la dépendance entre les deux critères, localisation et catégorisation de la population active.

Mesurer les différences

Nous avons admis dans l’article précédent que l’information donnée par chaque cellule de notre tableau est la différence entre ce qui était attendu et ce qui est. Nous allons à présent le mesurer.

Pour chaque cellule de notre tableau de fréquence nous allons calculer la quantité suivante :

(Réel – Attendu)² / Attendu

Cette distance est appelée métrique Khi 2. Elle est utilisée classiquement pour déterminer l’indépendance de deux critères de classification. Si la somme des distances calculées pour chaque cellule est inférieure à une certaine valeur (dépendante de la taille du tableau) alors les critères sont considérés comme indépendants.

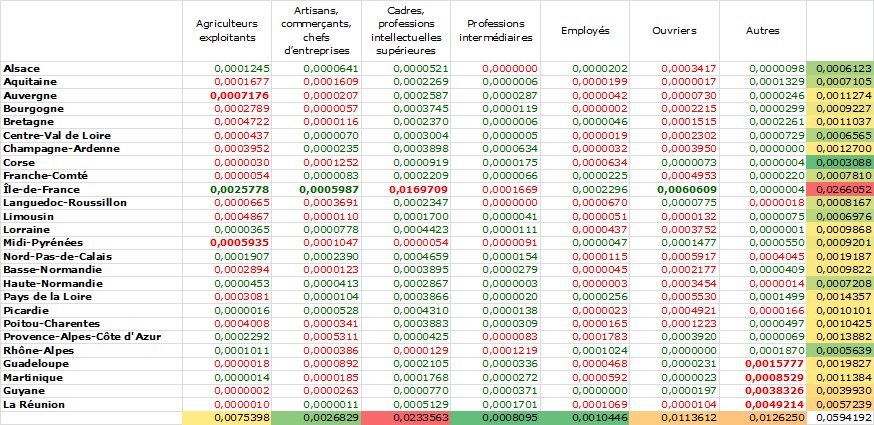
Faisons de calcul pour les ouvriers d’Île de France pour lesquels nous avions une fréquence attendu de 4,52% et une fréquence observée de 2,86% nous obtenons une distance de 0,00606.

Dans le tableau ci-dessus nous avons calculé toutes les distances puis nous avons additionné les distances en ligne et en colonne.

Sur les cellules de l’intérieur du tableau nous avons appliqué les formats conditionnels suivants : les cellules pour lesquels le réel est inférieur (resp. supérieur) à l’attendu sont écrites en vert (resp. rouge) et les 10 plus fortes valeurs sont écrites en gras. Pour les sommes marginales, on a simplement appliqué un gradient de couleur du vert pour la valeur la plus faible au rouge pour la plus forte.

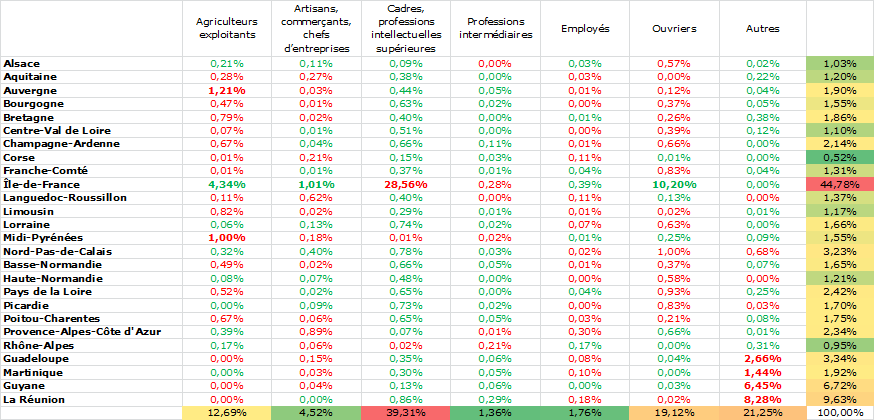
La visibilité est améliorée par un passage au pourcentage que représente chaque cellule par rapport au total.

Ce calcul de pourcentage nous donne la proportion exacte d’information contenue dans chaque cellule. Ainsi, nous constatons immédiatement que 28,56 % de l’information de tout le tableau vient de la surreprésentation des professions intellectuelles supérieures en Île de France. La deuxième cellule la plus porteuse d’information est celles des ouvriers d’Île de France, moins nombreux qu’attendus.

La sommation des pourcentages en ligne et en colonne nous indique la contribution de chacune des lignes et colonnes à l’information globale fournie par le tableau. On voit ainsi que les catégories employés et les professions intermédiaires qui représentent à elles deux plus de 50 % des effectifs contribuent très peu à l’information du tableau, environ 3 %. On peut tout de même en tirer la conclusion que la proportion que représentent ces catégories dans la population active est très faiblement influencée par la localisation, ce qui en soi est une information intéressante.

En mobilisant un bagage informatique et mathématique modeste, nous pouvons à présent mener une analyse systématique et rigoureuse des tableaux de contingence obtenus avec les tableaux croisés dynamiques.

Remercions-en Michel Volle inventeur de la méthode.